Weights
Many OnlineStats are parameterized by a Weight that controls the influence of new observations. If the OnlineStat is capable of calculating the same result as a corresponding offline estimator, it will have a keyword argument weight. If the OnlineStat uses stochastic approximation, it will have a keyword argument rate (see this great resource on stochastic approximation algorithms).
Consider how weights affect the influence of the next observation on an online mean $\theta^{(t)}$, as many OnlineStats use updates of this form. A larger weight $\gamma_t$ puts higher influence on the new observation $x_t$:
\[\theta^{(t)} = (1-\gamma_t)\theta^{(t-1)} + \gamma_t x_t\]
The values produced by a Weight must follow two rules:
- $\gamma_1 = 1$ (guarantees $\theta^{(1)} = x_1$)
- $\gamma_t \in (0, 1), \quad \forall t > 1$ (guarantees $\theta^{(t)}$ stays inside a convex space)
The notion of weighting in OnlineStats is fundamentally different than StatsBase.AbstractWeights.
- In OnlineStats, a weight determines the influence of an observation compared to the current state of the statistic.
- In StatsBase, a weight determines the influence of an observation in the overall calculation of the statistic.
julia> using OnlineStats, StatsBaseERROR: ArgumentError: Package StatsBase not found in current path. - Run `import Pkg; Pkg.add("StatsBase")` to install the StatsBase package.julia> x = 1:99;julia> w = fill(0.1, 99); # StatsBase: All weights == 0.1julia> mean(x) ≈ mean(x, aweights(w)) ≈ mean(x, fweights(w)) ≈ mean(x, pweights(w)) # OnlineStats: All weights == 0.1ERROR: UndefVarError: `aweights` not definedjulia> o = fit!(Mean(weight = n -> 0.1), x)Mean: n=99 | value=90.0003julia> mean(x) # Every observation has equal influence over statistic.50.0julia> value(o) # Recent observations have higher influence over statistic.90.00026561398887
Weight Types
OnlineStatsBase.EqualWeight — TypeEqualWeight()Equally weighted observations.
$γ(t) = 1 / t$
OnlineStatsBase.ExponentialWeight — TypeExponentialWeight(λ::Float64)
ExponentialWeight(lookback::Int)Exponentially weighted observations. Each weight is λ = 2 / (lookback + 1).
ExponentialWeight does not satisfy the usual assumption that γ(1) == 1. Therefore, some statistics have an implicit starting value.
# E.g. Mean has an implicit starting value of 0.
o = Mean(weight=ExponentialWeight(.1))
fit!(o, 10)
value(o) == 1$γ(t) = λ$
OnlineStatsBase.LearningRate — TypeLearningRate(r = .6)Slowly decreasing weight. Satisfies the standard stochastic approximation assumption $∑ γ(t) = ∞, ∑ γ(t)^2 < ∞$ if $r ∈ (.5, 1]$.
$γ(t) = inv(t ^ r)$
OnlineStatsBase.LearningRate2 — TypeLearningRate2(c = .5)Slowly decreasing weight.
$γ(t) = inv(1 + c * (t - 1))$
OnlineStatsBase.HarmonicWeight — TypeHarmonicWeight(a = 10.0)Weight determined by harmonic series.
$γ(t) = a / (a + t - 1)$
OnlineStatsBase.McclainWeight — TypeMcclainWeight(α = .1)Weight which decreases into a constant.
$γ(t) = γ(t-1) / (1 + γ(t-1) - α)$
Custom Weighting
The Weight can be any callable object that receives the number of observations as its argument. For example:
weight = invwill have the same result asweight = EqualWeight().weight = x -> .01will have the same result asweight = ExponentialWeight(.01)
julia> y = randn(100);julia> fit!(Mean(weight = EqualWeight()), y)Mean: n=100 | value=0.000430232julia> fit!(Mean(weight = inv), y)Mean: n=100 | value=0.000430232
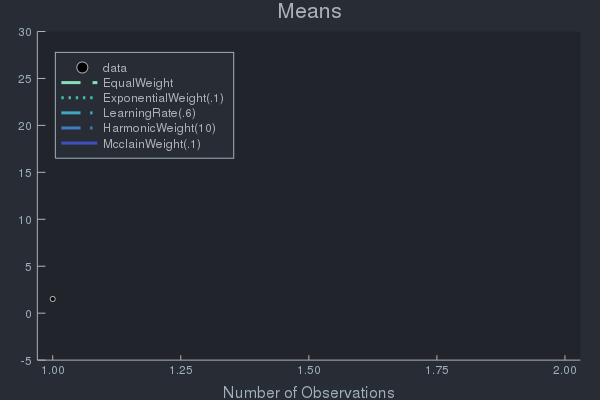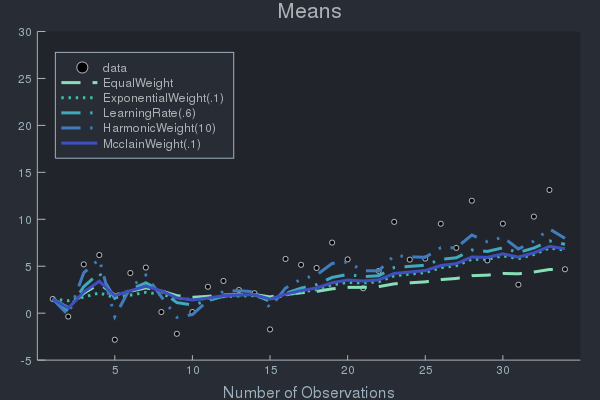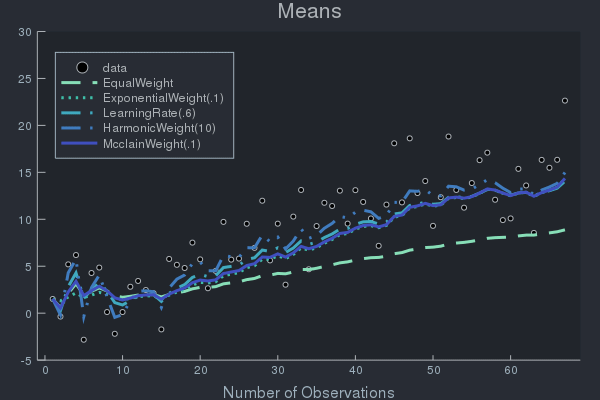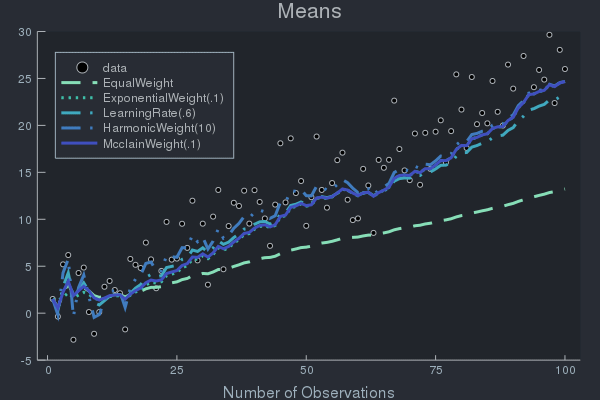
Example of Weight Effects using Data with Concept Drift